#P3906. Geodetic集合
Geodetic集合
题目描述
图 是一个无向连通图,没有自环,并且两点之间至多只有一条边。我们定义顶点 的最短路径就是从 到 经过边最少的路径。所有包含在 的最短路径上的顶点被称为 的 Geodetic 顶点,这些顶点的集合记作 。
我们称集合 为一个 Geodetic 集合。
例如下图中,,,。
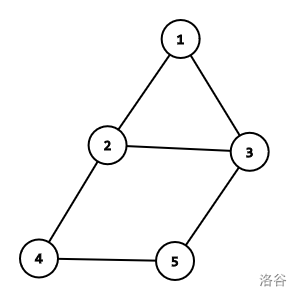
给定一个图 和若干点对 ,请你分别求出 。
输入格式
第一行为两个整数 ,分别表示图 的顶点数和边数(顶点编号为 )。
接下来 行,每行两个整数 ,表示 顶点 和 之间有一条无向边。
第 行有一个整数 ,表示给定的点对数。
接下来 行,每行两个整数 ,表示每个点对的起点和终点。
输出格式
共 行,对于输入文件中每一个点对 ,按顶点顺序一行输出 里面的所有点的编号。
5 6
1 2
1 3
2 3
2 4
3 5
4 5
3
2 5
5 1
2 4
2 3 4 5
1 3 5
2 4
提示
对于所有数据,满足 ,。
